Next: A Posteriori Guidance for Astronomical Images
Up: Applications
Previous: Image Processing of Digitized Spectral Data
Table of Contents -- Index -- PS reprint -- PDF reprint
A. F. Lanza, M. Rodonò1, U. Becciani and
V. Antonuccio Delogu
Osservatorio Astrofisico di Catania,
Viale A. Doria, 6 - I 95125 Catania, Italy
1Istituto di Astronomia dell'Università degli Studi di Catania,
Viale A. Doria, 6 - I 95125 Catania, Italy
Binary systems belonging to the RS CVn and BY Dra classes show huge cool spots on their photospheres which are regarded as manifestations of intense magnetic fields by analogy with sunspots (e.g., Tuominen et al. 1991, Strassmeier & Linsky 1996).
The analysis of sequences of light curves spanning a long time interval (at least one or two decades) allows us to detect activity cycles, analogous to the solar 11-year cycle, inferring the overall properties of the stellar dynamos. Moreover, long-term data can be used to estimate the effects of starspots on stellar parameters (Rodonò et al. 1995, Lanza et al. 1997).
We address the problem of modelling a long-term sequence of light curves adopting recently developed tools for parallel computing and using an inhomogeneous cluster of CPUs.
The reconstruction of the surface map of an active star by using photometric data alone is an ill-posed problem. It is possible to find a unique and stable solution if a priori assumptions on the properties of the picture elements (pixels) of the map are adopted such as the Maximum Entropy (hereinafter ME, e.g., Vogt et al. 1987) and the Tikhonov criteria (hereinafter T, e.g., Piskunov et al. 1990).
The optimized map is found by minimizing the objective function Q consisting
of a linear combination of the ![]() and the regularizing function S:
and the regularizing function S:
![]() The expressions for
The expressions for ![]() (which gives the deviation between the fluxes computed from the map and those observed) and the regularizing ME or T functions can be found in, e.g., Cameron (1992);
the Lagrange multiplier
(which gives the deviation between the fluxes computed from the map and those observed) and the regularizing ME or T functions can be found in, e.g., Cameron (1992);
the Lagrange multiplier ![]() measures the relative weights
of the a priori assumption and
measures the relative weights
of the a priori assumption and ![]() in constraining the
solution.
In our approach the best value of
in constraining the
solution.
In our approach the best value of ![]() is determined by the
distribution of the residuals between the observed and the computed fluxes
(Lanza et al. 1997; see also Cameron 1992). In any case several solutions are computed for different values of
is determined by the
distribution of the residuals between the observed and the computed fluxes
(Lanza et al. 1997; see also Cameron 1992). In any case several solutions are computed for different values of ![]() in order to find the optimal value through a suitable statistical test.
in order to find the optimal value through a suitable statistical test.
In the modelling of a light curve sequence it is also of interest to determine the physical parameters of the system components, which may be affected by the presence of spots. In such a case the overall computational problem may become much more complex and time consuming.
Our parallel procedure was written in standard FORTRAN using the PVM library
version 3 and exploits a networked system to
perform the analysis of a sequence of NL light curves. The procedure
starts on a main host - the master-host - and the single jobs
are automatically spawned on all the systems on which PVM is
available. This procedure actually generates a virtual machine (hereinafter VM).
We assign the modelling of each light curve with given values
of the system parameters and ![]() to a single system
(host) which, at the end of its task, sends the output back to the master-host.
to a single system
(host) which, at the end of its task, sends the output back to the master-host.
The minimization of the function Q for all the light curves of a given sequence,
for fixed values of the system parameters, represents a cycle of the procedure.
In general the analysis is not limited to one cycle because we
can be interested in the simultaneous determination of one or more system
parameters, such as
the luminosity ratio of the system (see Rodonò et al.
1995, Lanza et al. 1997).
Thus, considering a typical sequence consisting of a few tens
of light curves, a few hundred modelling steps
(i.e., Q minimizations) are required if ![]() is held fixed, and up to a few thousand if
is held fixed, and up to a few thousand if ![]() also is varied
(see also Wilson 1993).
also is varied
(see also Wilson 1993).
The procedure is implemented using a master/slave paradigm.
The master is the program controlling the execution of the
overall analysis and it is running on the master-host.
The master performs the following operations in sequence:
a) it identifies all available hosts and adds them to the VM;
b) it assigns the values to the system parameters and the ![]() 's
for the given cycle; c) it spawns each analysis of the cycle
on one of the hosts by choosing it according to the number of
normal points in the
light curve and the current weights assigned to the hosts;
d) it periodically checks whether all the hosts of the VM are
running and, in case of a fault, restarts the lost jobs;
e) it receives the output files from the hosts which have completed their jobs
and updates their current weights; f) at the end of the cycle, according to the
task assigned, it ends the execution or starts a new cycle
from step b).
's
for the given cycle; c) it spawns each analysis of the cycle
on one of the hosts by choosing it according to the number of
normal points in the
light curve and the current weights assigned to the hosts;
d) it periodically checks whether all the hosts of the VM are
running and, in case of a fault, restarts the lost jobs;
e) it receives the output files from the hosts which have completed their jobs
and updates their current weights; f) at the end of the cycle, according to the
task assigned, it ends the execution or starts a new cycle
from step b).
The estimate of the weight of each host is initially based on the time it takes to analyse a reference light curve and is updated in the course of the calculation using the elapsed times of the previous analyses.
If a task is anomalously ended, the master detects the fault and tries to restart it on the same host. If the fault occurs again or the host is not available, the master deletes the host from the VM, and the analysis is re-scheduled on the first available free host. After a user-defined period, a deleted host can be checked again and, if it is found available, it can be added again to the VM. Therefore the VM configuration changes dynamically and automatically during the run with hosts being added or deleted by the master according to their current availability status.
We have performed several tests on the workstation cluster of Catania Astrophysical Observatory analysing a sequence of 18 light curves of the eclipsing binary AR Lacertae (see Lanza et al. 1997).
The purpose of a first test (linear test) has been to
study the variation of the
computational complexity, as a function of the number of data points in the
light curve. Only one processor has been used to run the
procedure. It has been a SuperSparc+ processor (clockspeed 50 MHz)
and all the results are reported assuming it as the
reference processor.
As workstation operating system we used Solaris 2.5
and 64 MB RAM were allocated during the entire execution time.
The results are shown in Figure 1a. There is evidence that
the execution time, and thus the computational complexity,
increases linearly with the number of data points in the analysed light curve.
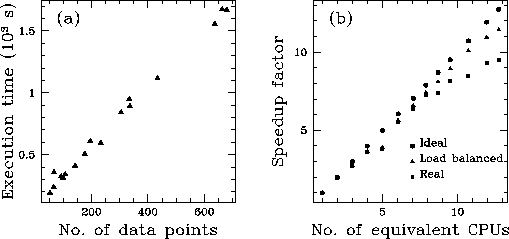 |
In a second test, we analysed a sequence of 18 light curves running in parallel 4 cycles
each with a different value of the luminosity ratio and a fixed ![]() ,adopting the ME regularization. With this test we sampled the parameter space to optimize the luminosity ratio of the components of the system.
The number
of processors forming the VM has been increased step by step to find
how the speedup increases as a function of the number of CPUs. The results
of the test are reported in Figure 1b in terms of
equivalent processors, the reference processor being the
CPU SuperSparc+ 50 MHz with SPECint92=76.9 and SPECfp92=80.1.
,adopting the ME regularization. With this test we sampled the parameter space to optimize the luminosity ratio of the components of the system.
The number
of processors forming the VM has been increased step by step to find
how the speedup increases as a function of the number of CPUs. The results
of the test are reported in Figure 1b in terms of
equivalent processors, the reference processor being the
CPU SuperSparc+ 50 MHz with SPECint92=76.9 and SPECfp92=80.1.
We plot in Figure 1b also the speedup expected for an ideal cluster and a perfectly balanced application,
which assumes that all the CPUs begin and end their jobs simultaneously. This case can be realized only on a dedicated cluster.
We see that there is no significant
degradation of the overall performance
with only a slight tendency toward a saturation when the number of CPUs
exceeds ![]() . This is also a consequence of the
fact that the processors we used are rather similar (the maximum difference in
their scaled powers is less than 20-25%).
. This is also a consequence of the
fact that the processors we used are rather similar (the maximum difference in
their scaled powers is less than 20-25%).
We have presented a very general and simple procedure which exploits a cluster of inhomogeneous computers to significantly speed up the modelling of a sequence of light curves. The same procedure, with only minor modifications, can be applied also to the modelling of spectroscopic or polarimetric data (see, e.g., Milone 1993, Vincent et al. 1993).
Our procedure can use a simple Workstation cluster, not necessarily dedicated, or medium-large parallel systems having a message passing software as PVM. In the near future we plan to produce also an MPI version with an X-based user interface to monitor processing and make it available as a public domain software for light curve or Doppler Imaging analysis.
Cameron A. C., 1992, in P. B. Byrne, D. J. Mullan (Eds.) LNP 397, (Berlin: Springer-Verlag), 33
Lanza A. F., et al., 1997, A&A, submitted
Milone E. F. (Ed.), 1993, Light curve modelling of eclipsing binary stars, (Berlin: Springer-Verlag)
Piskunov N. E., Tuominen I., Vilhu O., 1990, A&A, 230, 363
Rodonò M., Lanza A. F., Catalano S., 1995, A&A, 301, 75
Strassmeier K. G., Linsky J. L. (Eds.), 1996, IAU Symp. 176, (Dordrecht: Kluwer)
Tuominen I., et al. (Eds.), 1991, IAU Coll. 130, (Berlin: Springer-Verlag)
Vincent A., Piskunov N. E., Tuominen I., 1993, A&A, 278, 523
Vogt S. S., Penrod N. E., Hatzes A. P., 1987, ApJ, 321, 496
Wilson R. E., 1993, PASP, 106, 921
Next: A Posteriori Guidance for Astronomical Images
Up: Applications
Previous: Image Processing of Digitized Spectral Data
Table of Contents -- Index -- PS reprint -- PDF reprint